OpenAI 与 DeepSeek 卷得不可开交的时候,谷歌 DeepMind 的数学推理模型又偷偷惊艳了所有人。
在最新的一篇论文中,谷歌 DeepMind 介绍了全新进化的 AlphaGeometry 2,该系统在解决奥林匹克几何问题方面已经超过了金牌得主的平均水准。

论文标题:Gold-medalist Performance in Solving Olympiad Geometry with AlphaGeometry2
论文链接:https://arxiv.org/pdf/2502.03544
国际奥林匹克数学竞赛(IMO)是一项面向全球高中生的著名数学竞赛。IMO 问题以难度大著称,解决这些问题需要对数学概念有深刻理解,并能创造性地应用这些概念。几何是 IMO 四大题型之一,各题型之间最为统一,非常适合基础推理研究。因此,这项赛事也成为了衡量人工智能系统高级数学推理能力的理想基准。
在 2024 年 7 月,谷歌 DeepMind 曾经介绍了 AlphaGeometry (AG1),这是一个神经符号系统,在 2000-2024 年 IMO 几何问题上的解题率达到 54%,距离金牌也只有一步之遥。AG1 将语言模型 (LM) 与符号引擎相结合,有效地解决了这些具有挑战性的问题,造就了数学领域的「AlphaGo 时刻」。
尽管 AG1 取得了成功,但它在几个关键领域仍存在局限性。其性能受限于特定领域语言的范围、符号引擎的效率以及初始语言模型的容量。因此,在考虑 2000 年至今的所有 IMO 几何问题时,AG1 只能达到 54% 的解题率。
最新的这篇论文介绍了 AlphaGeometry2(AG2),它是解决了这些限制的升级版本,并显著提高了性能。AG2 利用了更强大的基于 Gemini 的语言模型,该模型是在一个更大、更多样化的数据集上训练出来的。团队还引入了速度更快、更强大的符号引擎,并进行了优化,如减少规则集和增强对二重点的处理。此外,团队还扩展了领域语言,以涵盖更广泛的几何概念,包括轨迹定理(locus theorem)和线性方程(linear equation)。
为了进一步提高性能,他们开发了一种新型搜索算法,可探索更广泛的辅助构造策略,并采用知识共享机制来扩展和加速搜索过程。最后,他们在建立一个用自然语言解决几何问题的全自动可信赖系统方面取得了进展。为此,谷歌利用 Gemini 将问题从自然语言翻译成 AlphaGeometry 语言,并实施了新的自动图解生成算法。
这些改进最终大大提高了性能:AG2 在 2000-2024 年 IMO 所有几何问题上的解题率达到了令人印象深刻的 84%,这表明人工智能在处理具有挑战性的数学推理任务方面实现了重大飞跃,并超越了 IMO 金牌得主的平均水准。
核心提升如下:
扩展领域语言:涵盖轨迹型定理、线性方程和非构造性问题陈述;
更强更快的符号引擎:优化了规则集,增加了对二重点的处理,以及更快的 C++ 实现;
先进新颖的搜索算法:利用知识共享的多搜索树;
增强的语言模型:利用 Gemini 架构在更大和更多样化的数据集上进行训练。
更强、更快的符号引擎
符号引擎是 AlphaGeometry 的核心组件,谷歌称之为演绎数据库算术推理(Deductive Database Arithmetic Reasoning,DDAR)。它是一种计算演绎闭包的算法,即给定一组核心初始事实的所有可演绎事实集合。DDAR 遵循一组固定的演绎规则来构建此演绎闭包,并迭代地将新的事实添加到演绎闭包中,直到无法再添加。
DDAR 驱动语言模型的训练数据生成以及测试时证明搜索期间的演绎步骤搜索。在这两种情况下,速度都至关重要。更快的数据生成可以达成更大规模、更积极的数据过滤,而更快的证明搜索可以实现更广泛的搜索,从而增加给定时间预算内找到解决方案的可能性。
DDAR 有以下三项主要改进:
处理二重点(double ponit)的能力;
更快的算法;
更快的实现。
处理二重点
在重新实现 DDAR 时,谷歌试图保持与原始算法大致相同的逻辑强度,只是由于实现差异而稍微强一些(例如泰勒斯定理被更通用的圆心角定理取代)。然而,DDAR 缺少一个对解决难题至关重要的关键特性:它无法接受两个名称不同但坐标相同的点。
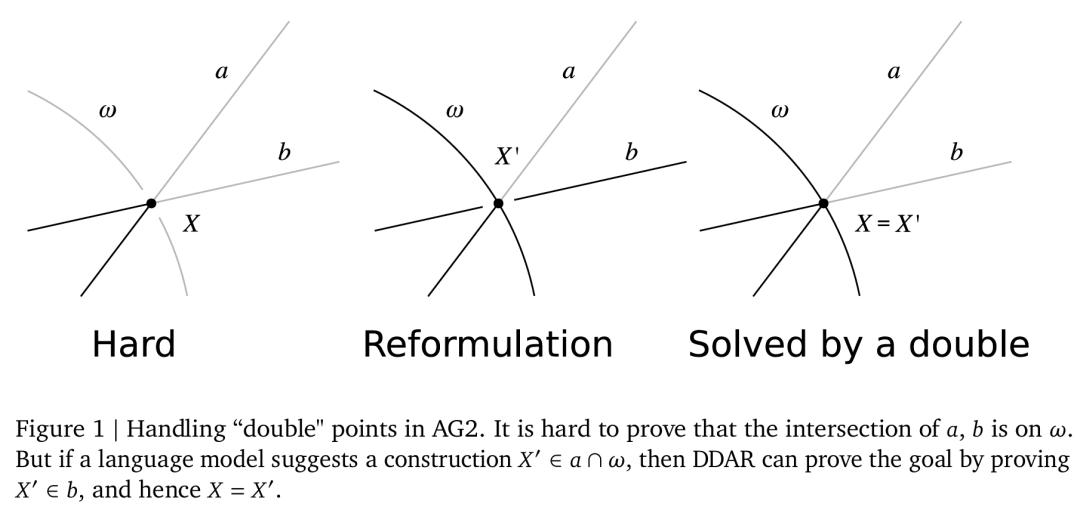
例如,想象一个问题:在点 �� 处两条线 ��,�� 相交,并打算证明 �� 位于某个圆 �� 上。最合理的方法可能是重构,不证明 ��,�� 的交点在 �� 上,而是证明 ��,�� 的交点在 �� 上。这是等效的,但更容易证明,因为可以在圆上移动角度。具体可参见图 1。
要对双重点推理实现这种重构,需要执行以下四个步骤:
构造一个新点��′作为 ��,�� 的交点(不知道 ��′ 是否与 �� 重合)。这是一个辅助构造,必须由语言模型预测;
证明��位于��上;
由于��和��′都位于��,��上,得出�� = ��′;
因此��位于��上。
更快的算法
DDAR 算法可以处理一系列规则,并尝试将每条规则应用于所有点的组合。此过程涉及以下两个部分:
候选搜索步骤,它的时间复杂度是点数的多项式;
子句匹配步骤,它的时间复杂度是每个前提的子句数的指数。
理论上,在 AG1 中搜索相似三角形候选的最坏情况是 ��(��^8),这是最耗时的步骤之一。指数级子句匹配是另一个成本高昂的步骤。
DDAR 最耗时的两个部分是搜索相似三角形和搜索圆内接四边形。在 AG2 中,谷歌设计了一种改进的 DDAR2 算法。对于相似三角形,他们遍历所有的点三元组,对它们的「形状」进行哈希处理。如果两次识别出形状,则检测出相似的对。
对于圆内接四边形,谷歌遍历所有对(点��、线段����),并对(��,��,∠������)的值进行哈希处理。如果这样的三元组重复出现,就得到一个圆内接四边形。线段 ���� 或 ∠������ 的「值」是指 AR 子模块计算出的符号范式。该子模块跟踪角度、距离和对数距离之间的已知线性方程,了解其代数结果,并将任何线性表达式简化为其标准范式。
更快的实现
虽然新算法已经显著加快了 DDAR 的速度,但谷歌使用 C++ 实现其核心计算(高斯消元法),从而进一步提升了速度。
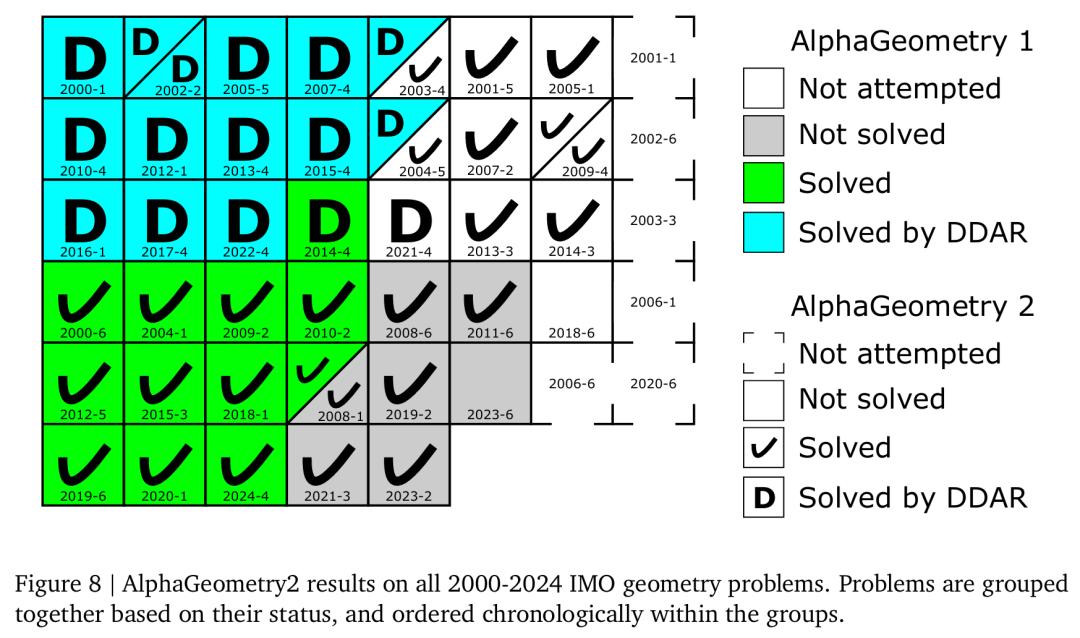
新的 C++ 库通过 pybind11 导出到 Python,速度是 DDAR1 的 300 多倍。为了对速度改进进行基准测试,谷歌选择了一组 25 道 DDAR 无法解决的 IMO 问题(见图 8),并在配备 AMD EPYC 7B13 64 核 CPU 的机器上运行测试 50 次。
结果显示,DDAR1 平均可以在 1179.57±8.055 秒内完成计算,但 DDAR2 的速度要快得多,在 3.44711 ± 0.05476 秒内完成。
更好的合成训练数据
与 AG1 类似,谷歌使用的合成数据生成方法从随机图采样开始,并使用符号引擎从中推断出所有可能的事实。并且对于每个推断出的事实,他们都使用回溯算法来提取可以证明事实的相应前提、辅助点和推理步骤。
谷歌的数据生成方法刻意避免使用人为设计的问题作为初始图种子,并严格从随机图开始。这种设计选择消除了数据污染的风险,并允许探索可能超出现有人类知识的定理分布。
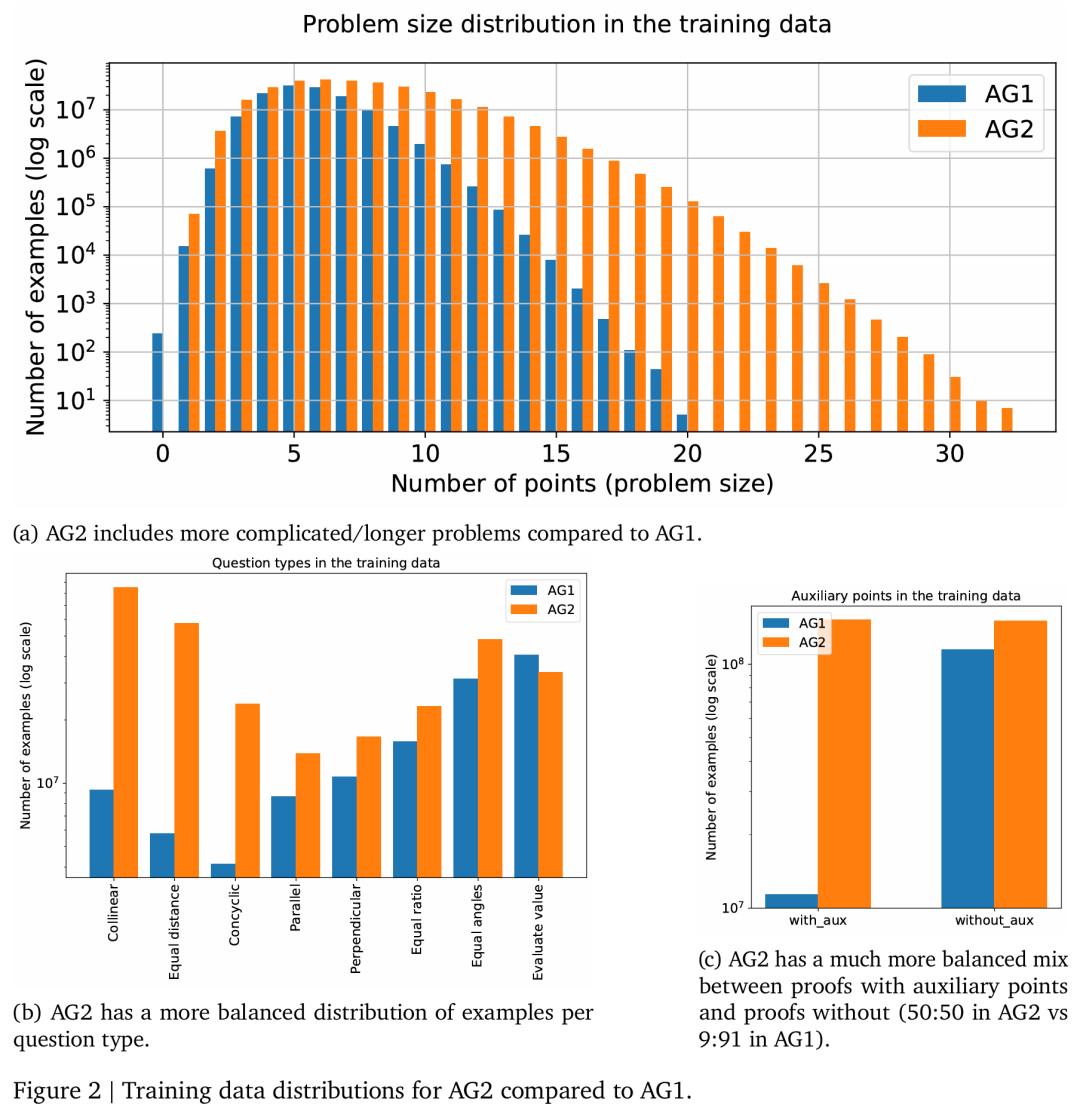
更大、更复杂的图表和更好的数据分布。首先,谷歌扩大数据生成的来源,并更仔细地重新平衡数据分布。图 2 展示了 AG2 与 AG1 的训练数据比较:
探索两倍大小的随机图,从而提取更复杂的问题;
生成的定理复杂了两倍,即点和前提的数量;
生成的证明复杂了 10 倍,即证明步骤多 10 倍;
问题类型之间的数据分布更均衡;
有无辅助点的问题之间的数据分布更均衡。
更快的数据生成算法。谷歌还提升了数据生成算法的速度。回想 AG1,谷歌首先在随机图上运行演绎闭包,然后回溯以获得可以证明闭包中每个事实的最小问题和最小证明。为了获得 AG1 中的最小问题,必须从问题中彻底删除不同的点子集,然后重新运行 DDAR 以检查可证明性。这样的搜索可以找到基数最小的子集,但是作为指数级搜索,对于大量的点而言不可行。
因此,谷歌切换到图 3 所示的贪婪丢弃算法,该算法仅使用线性数量的检查来判断一组点是否足以证明目标。只要检查是单调的(如果 �� ⊆ ��,则 check_provable (��) ⇒ check_provable (��)),贪婪算法就保证找到一组关于包含(inclusion)的最小点集。

新颖的搜索算法
在 AG1 中,谷歌使用简单的束搜索来发现证明。在 AG2 中,他们设计了一种新颖的搜索算法,可以并行执行多个不同配置的束搜索,并允许它们通过知识共享机制互相帮助,具体可见图 4。为了提高系统的稳健性,谷歌还为每个搜索树配置使用多个不同的语言模型。这种搜索算法被称为搜索树的共享知识集合(Shared Knowledge Ensemble of Search Trees,SKEST) 。
该搜索算法的工作原理如下所示:在每个搜索树中,一个节点对应于一次辅助构造尝试,然后是一次符号引擎运行尝试。如果尝试成功,所有搜索树都会终止。如果尝试失败,节点将把符号引擎设法证明的事实写入共享事实数据库。这些共享事实经过过滤,使它们不是特定于节点本身的辅助点,而仅与原始问题相关。这样一来,这些事实也可以对同一搜索树中的其他节点以及不同搜索树中的节点产生助益。
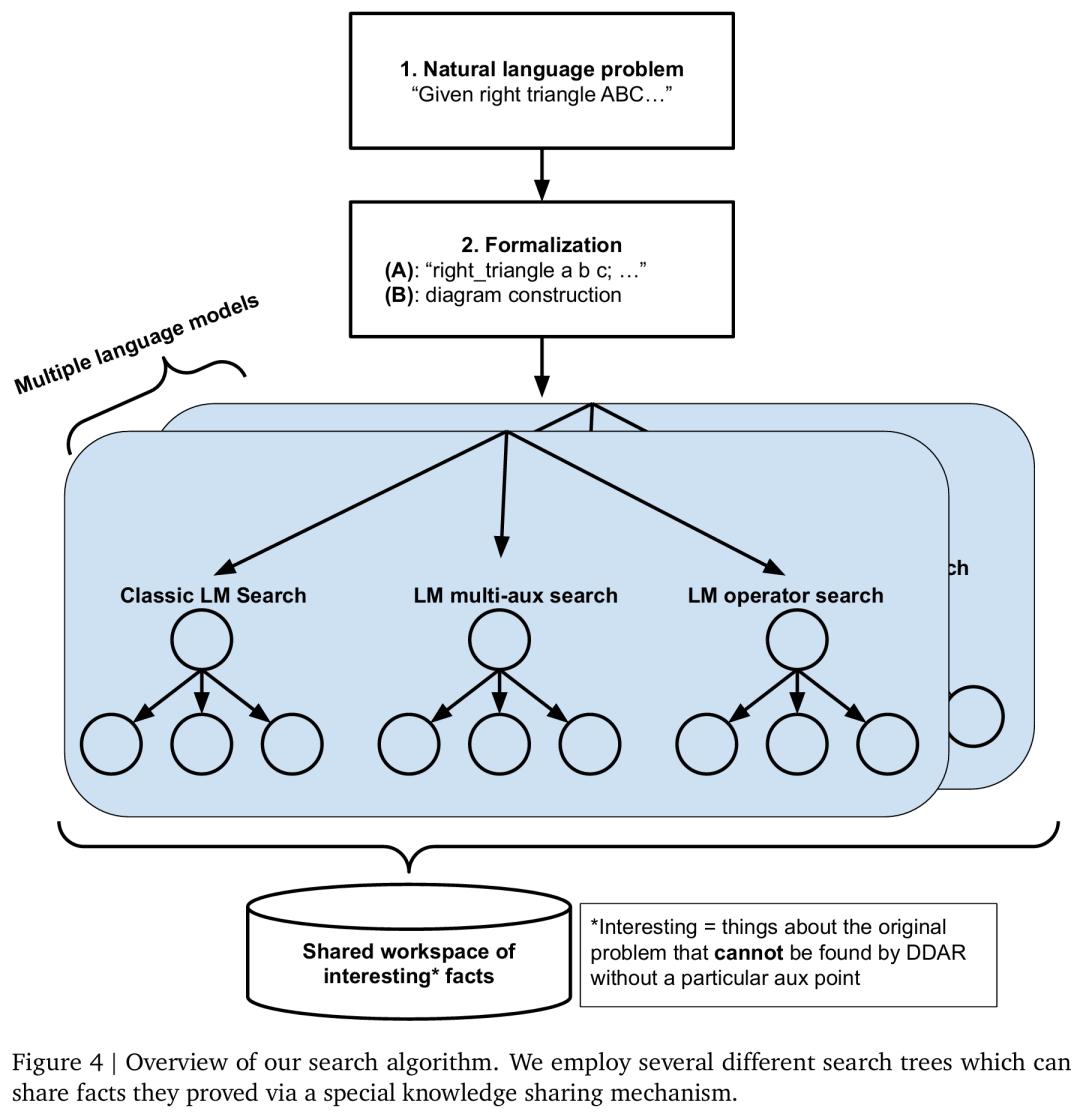
系统设计细节。对于证明搜索,谷歌使用 TPUv4 为每个模型提供多个副本,并让同一模型内的不同搜索树根据自身的搜索策略来查询同一服务器。除了异步运行这些搜索树之外,谷歌还对 DDAR 工作器与 LM 工作器进行异步运算,其中 LM 工作器将它们探索的节点内容写入数据库,DDAR 工作器异步拾取这些节点并尝试它们。DDAR 工作器之间相互协调,以确保它们平等分配工作。单个 DDAR 工作器池在不同问题之间共享(如果一次解决多个问题),这样先前解决的问题就会为正在解决的其余问题释放自己的 DDAR 计算资源。
更好的语言模型
AG2 的最后一项改进是使用新的语言模型。下面将讨论全新的训练和推理设置。
训练设置
AG1 是一种定制版 Transformer,以无监督方式分两个阶段进行训练:先对有无辅助结构的问题进行训练,然后仅对包含辅助结构的问题进行训练。
对于 AG2,谷歌利用了 Gemini 训练流程并将训练简化为一个阶段:对所有数据进行无监督学习。他们使用了一种基于稀疏混合专家(MoE)Transformer 的新模型,该模型以 Gemini 1.5 为基础,并使用 AG2 数据进行训练。
谷歌使用以下三种设置来训练不同大小的多个模型:
1. 使用领域特定语言中的自定义 tokenizer 从头开始训练(AG1 设置);
2. 使用自然语言微调已经预训练的自定义专业数学 Gemini 模型;
3. 使用额外的图像输入(给定几何题的图表)从头开始进行多模态训练。
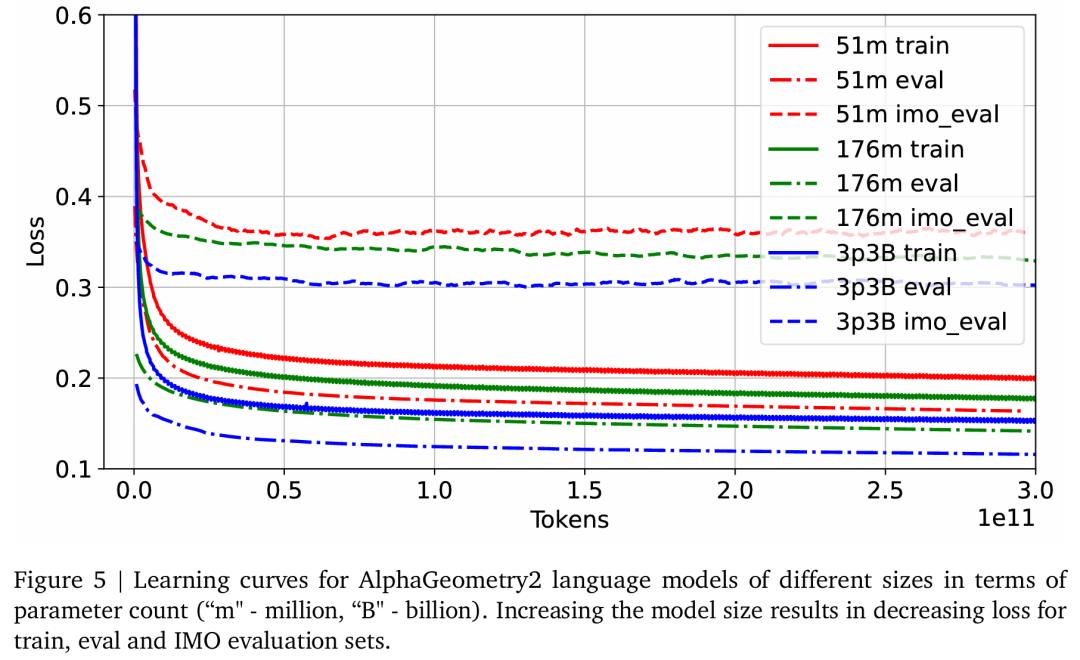
谷歌使用 TPUv4,并以硬件允许的最大批大小训练模型。学习率计划是先线性预热,然后余弦退火。学习率超参由 scaling 定律确定。在图 5 中,他们展示了基于参数量的不同大小的 Gemini 的学习曲线。正如预期的那样,增加模型大小会降低训练、评估以及特殊 IMO 评估集的困惑度损失。
推理设置
在 AG2 中,谷歌在提出辅助构造之前让 LM 了解 DDAR 所做的推论,进而丰富这个神经符号接口。也就是说,他们将以下信息输入到 LM 中
��_1:给定原始问题前提,DDAR 可推导出的事实集;
��_2:给定原始问题前提并假设目标谓词也为真,DDAR 可推导出的事实集;
��_3:数字正确的事实集(检查图表)。
竞赛结果
本文的主要下游指标是 IMO 几何题的解决率。2000-2024 年 IMO 共有 45 道几何题,谷歌将它们转化为了 50 道 AlphaGeometry 问题(称该集合为 IMO-AG-50)。
图 8 展示了主要结果,AlphaGeometry2 解决了 2000-2024 年 IMO 所有 50 道几何题中的 42 道,从而首次超越了金牌得主平均水平。

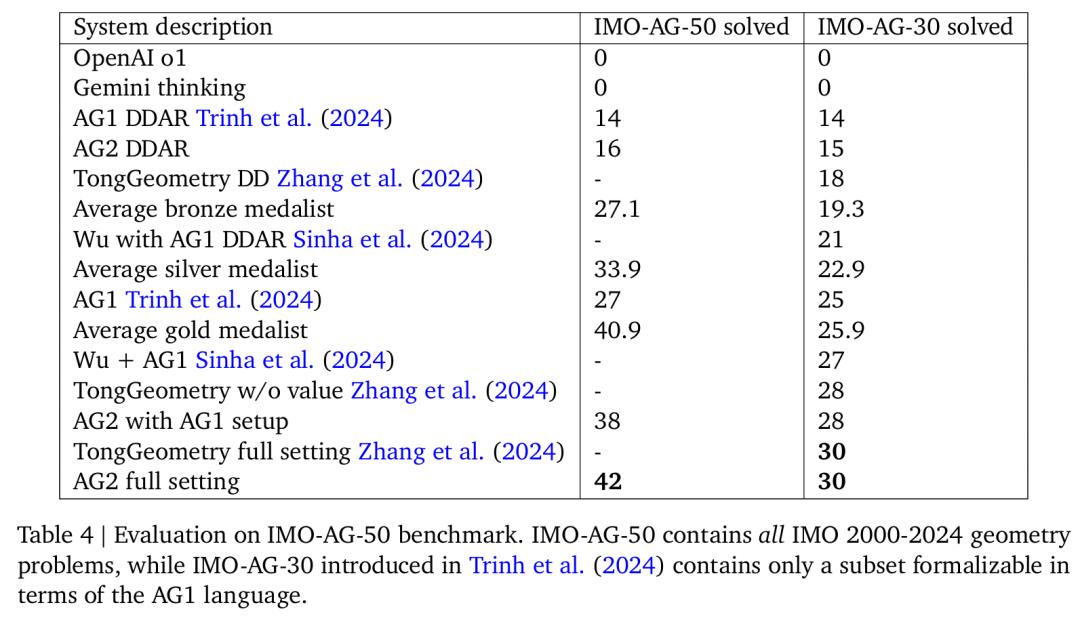
表 4 中提供了更多详细信息,其中将各种 AG2 配置与其他系统进行了比较。可以看到,AG2 实现了 SOTA。
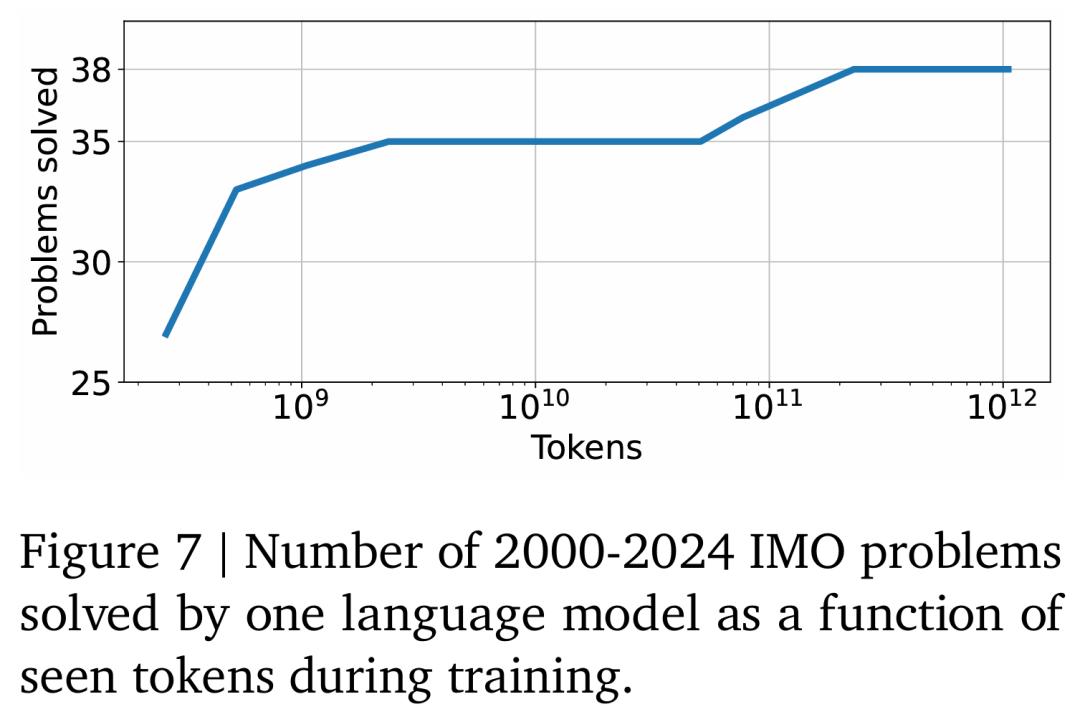
在图 7 中,针对通过前文「经典」树搜索与 DDAR 耦合的一个语言模型,谷歌将 IMO 解决率表示为了训练时函数(训练期间看到的 tokens)。有趣的是,AG2 仅在批大小为 256 时的 250 个时间步后(或者大约 2 亿 tokens),就解决了 50 道几何题中的 27 道。
谷歌还对推理设置如何影响整体性能进行了消融实验,结果如图 9 所示。他们发现,对于单个搜索树,最优配置是束大小 128、束深度 4 以及样本 32。